Introduction
Do you often find yourself wondering what is the difference between euclidean distance and cosine distance? How many sleepless nights have you had trying to classify your books as either cat books or dog books? Do you have difficulty estimating a dogs age? Do you like vague quotes, badly phrased answers and reading python scripts? Well then my friend, if the path be beautiful, let us not ask where it leads . .
Dimensional Chaos
Don’t listen to your friends when they tell you there is a single best way to calculate the distance between points in n-dimensional space. Depending on the problem, different measures will produce better results, and having the ability to pull these solutions out of your back pocket will serve you well. The following examples run through two scenarios, the first scenario details a problem where euclidean distance is the right solution, the second scenario details a problem where cosine distance is the correct solution. If you’d like to read the maths and python code, you can find my supplementary notebook stored here
I’m not a mathematician, in fact, I had to use autocorrect to even spell mathematician, so my definitions may not be textbook, but they may interest you enough to do your own research and understand a more grown up definition.
Euclidean distance is the as the crow flies distance between two points in space. If you grabbed your ruler and your pencil, and connected two points, the distance of that connecting line is your euclidean distance.
Cosine distance measures the cosine of the angle between lines drawn from two given points to a common origin, or more simply put - given an origin, how far do you have to stray from the path to one point to end up at the other. It is the great equalizer when the magnitude of a points values are not important.
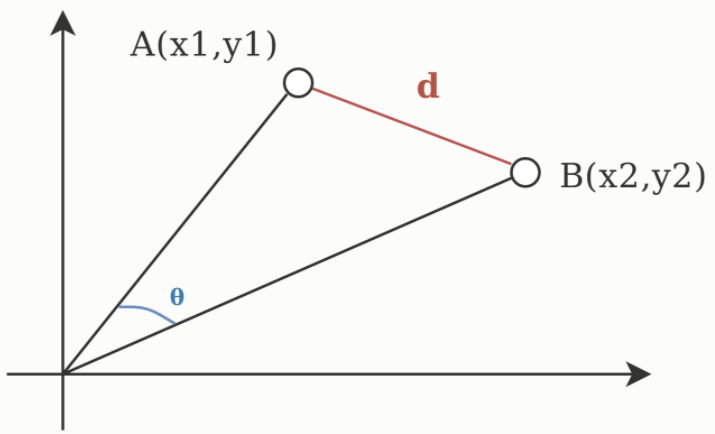
The above is a visual representation of euclidean distance (d) and cosine distance (θ). While cosine looks at the angle difference between two points from a common origin, euclidean distance measures the physical distance between the points.
Cosine distance? Surely you mean cosine similarity?
Sure look, you read it whatever way you want. Generally speaking a high cosine similarity score means two documents are similar, I’ve just subtracted the similarity score from 1 to give me the distance (or measure of how different they are).
Why not just look at points on a graph and kinda eyeball it
Sounds good in theory, but this solution can only work in a 1 - 3 dimensional solution and cannot scale. As simple humans we observe the world in 3 dimensional space, but in reality we encounter a lot of n-dimensional problems. Think of the last time you played Top Trumps - you can’t judge a dinosaur by its killer rating alone, you need to factor in things like height, weight, length, intelligence and age. To plot these points on a graph you would need a 6 dimensional graph. We can do the maths but we simply can not display 6 dimensions in a 3 dimensional world.

If you say so Shane . .
Chapter one - labradors
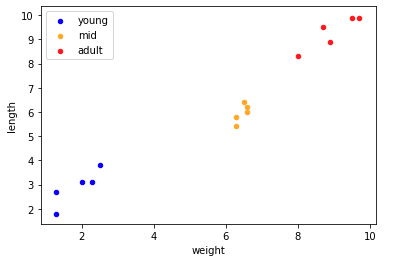
In this example we have a list of labradors, represented as a matrix. Each row represents a single dog, with each column representing one of the dogs attributes - namely Weight, Length and Age, where age can be one of three possible values - 0 (young), 1 (mid) or 2 (adult)
| index | weight | length | label |
|---|---|---|---|
| 0 | 6.6 | 6.2 | 1 |
| 1 | 9.7 | 9.9 | 2 |
| 2 | 8.0 | 8.3 | 2 |
| 3 | 6.3 | 5.4 | 1 |
| 4 | 1.3 | 2.7 | 0 |
| 5 | 2.3 | 3.1 | 0 |
| 6 | 6.6 | 6.0 | 1 |
| 7 | 6.5 | 6.4 | 1 |
| 8 | 6.3 | 5.8 | 1 |
| 9 | 9.5 | 9.9 | 2 |
| 10 | 8.9 | 8.9 | 2 |
| 11 | 8.7 | 9.5 | 2 |
| 12 | 2.5 | 3.8 | 0 |
| 13 | 2.0 | 3.1 | 0 |
| 14 | 1.3 | 1.8 | 0 |
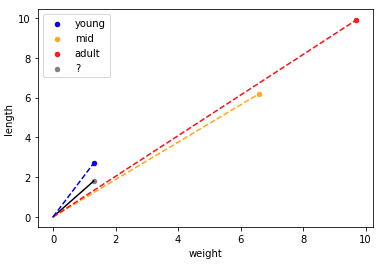
We’ll plot our points on a graph
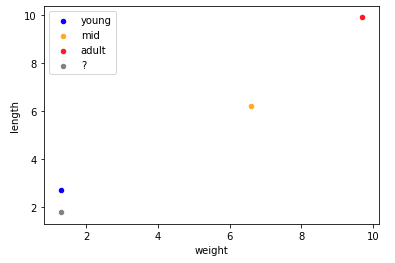
Next we’ll take one sample from each cluster (points 0,1 and 4), and we’ll take another point at random (point 14), strip its label and see if we can figure it out again using some fun maths.
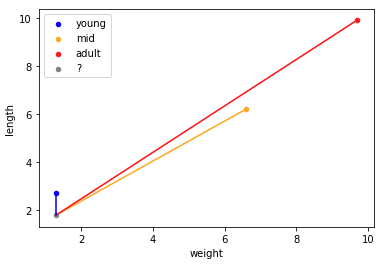
Using straight lines, we’ll connect our mystery point to each of the sample points, and essentially make a prediction based on the length of the line.
| point | label | distance |
|---|---|---|
| 4 | young | 0.9 |
| 0 | mid | 6.8 |
| 1 | adult | 11.6 |
Based on these results, we can see the nearest point is point 4 which if we check our table above, is labelled as 0 (young). This is a correct prediction !
But what would have happened if we used cosine distance ?
| point | label | distance |
|---|---|---|
| 1 | adult | 0.011 |
| 4 | young | 0.015 |
| 0 | mid | 0.018 |
We would have labelled our tiny dog as an adult ! The path from our origin to young was a much bigger diversion from the path to our mystery point than the path from our origin to adult. This makes sense when we look back to the earlier definition about cosine not really caring about the magnitude of our values. When looking at labradors, it seems obvious and logical that the longer and heavier the labrador is, the older it is.
Chapter two - a day at the library
So now you’re thinking, perfect, lets throw this cosine distance stuff in the bin and just euclidean distance all the things, but unfortunately you’d be in big trouble if you done that, because now you need to classify your book collection and euclidean distance is about to hit you hard. Lets take this sample book collection:
| document | dog count | cat count | label |
|---|---|---|---|
| hello kitty goes to space | 5 | 10 | cat |
| top ten cat facts | 1 | 4 | cat |
| how to pet a dog | 25 | 5 | ? |
| alien vs lassie | 60 | 8 | dog |
The table shows the title of the book, the number of times the word dog is mentioned, the number of times cat is mentioned and the current books class/label. We need to determine if how to pet a dog is a book about dogs or a book about cats. We tried to read it, but there were no doggy pictures in there so we gave up. Lets leave this to a machine. Now as we mentioned before, we can’t visualize n-dimensional space but we can still conceptualize it and perform mathematical operations that scale to meet the number of dimensions. So you might be thinking just take the bigger number but I refer you again to the top trumps example from earlier, we need a solution that scales. This 2 dimensional example is just for illustration purposes.
Alright Matilda, forget about the dinosaurs, and lets back to the books.
We use the word frequencies to plot our points on a graph
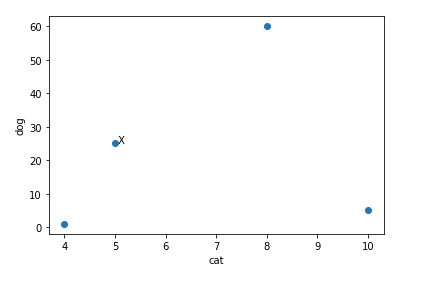
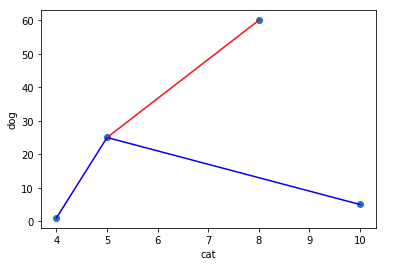
Using straight lines, we’ll connect our mystery point to each of the other points, and essentially make a prediction based on the length of the line.
| point | label | distance |
|---|---|---|
| 0 | cat | 20.6 |
| 1 | cat | 24 |
| 3 | dog | 35.1 |
Based on these results, we can see the nearest point is point 0 which if we check our table above, is labelled as cat. This is not a good prediction ! Why would a book titled how to pet a dog be labelled as cat?
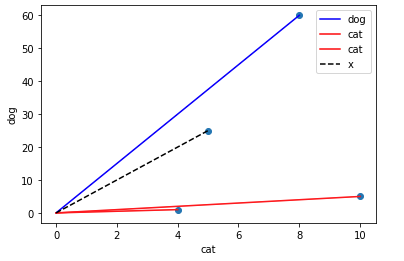
So what would have happened if we had used cosine distance instead?
| point | label | distance |
|---|---|---|
| 3 | dog | 0.002 |
| 0 | cat | 0.386 |
| 1 | cat | 0.571 |
This looks good, the nearest point is point 3 which is labelled as dog. This means we did not have to stray far from the path of the dog to end up at our mystery point.
Conclusion
There are so many rabbit holes and tangents when it comes to even the most basic machine learning problem. Hopefully I haven’t made things even more confusing. If nothing else, remember that in life the path of the dog is not always the way.
